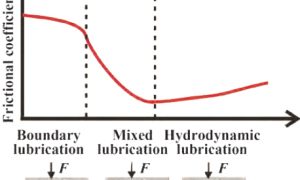
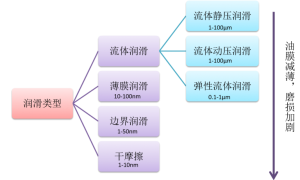
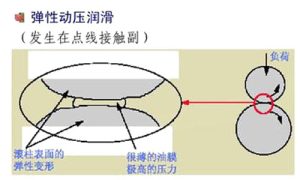
依靠运动副两个滑动表面的形状,在相对运动时产生收敛型油楔,形成具有足够压力的流体膜,从而将表面分隔开,这种润滑状态称为流体动压润滑。
1883年,托尔首先观察到采用油浴润滑的火车轴轴承中在运动时产生流体动压力,足以将轴承壳体的油孔中的油塞顶出。1886年,雷诺应用流体动力学中纳维—斯托克斯方程推导出流体润滑油膜压力分布的方程,称雷诺方程,从而为流体动压润滑理论奠定了基础。
流体动压润滑系统的主要特性如下:
1)对运动的阻力主要来自流体的“内摩擦”,也就是流体在外力作用下的流动过程中,在流体分子之间的内摩擦,即流体膜的剪切阻力或粘度。为了确定流体的粘度,17世纪时牛顿曾经提出了粘度流动定律,如下图所示。
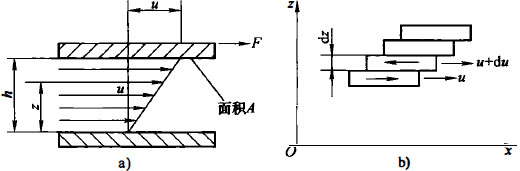
在两块距离为h的平行板中有粘性流体时,下表面保持固定,而上表面以速度u平行于下表面移动。当速度不太高时,因为流体分子粘附在表面上,流体相邻层的流动相互平移以层流状流动,这时为保持上表面移动所需要的力F与表面面积A以及所发生的剪切率成正比。由此可得:流体层间的切应力与剪切率成正比。也可按图1-2b所示模型写成:
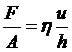
即如果在垂直高度间每一层按线性增加一个速度增量du。上表面的切应力与剪切率(或速度梯度)du/dz成正比。由此得:
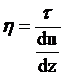
式中η——运动粘度(Pa•s)。
动力粘度又称绝对粘度,随流体的温度与压力的变化而改变,有时也随着剪切率的变化而改变。一般称遵从粘性切应力与剪切率成比例规律的流体为牛顿流体,而不遵从此规律的流体为非牛顿流体。在以下的分析中,均以润滑油作为流体。
2)两个滑动表面的几何形状在相对运动时产生收敛型油楔,形成足够的承载压力,从而将两表面分隔开,降低其摩擦与磨损。
如果对偶表面是完全平行的,在整个轴承中压力保持恒定,不能依靠改变分布图而在流体膜中产生压力来承受负载。但当轴承温度升高时,会使表面受热膨胀,引起流体膜收敛,还会使润滑剂的粘度改变而引起速度曲线的扭曲,改变油膜承载压力。